트리(Tree)

Tree

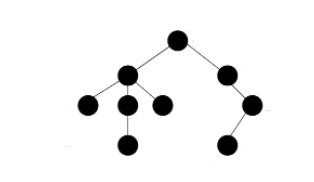
트리는 스택이나 큐와 같은 선형 구조가 아닌 계층적 관계를 표현하는 비선형 자료구조이다.

트리의 특징

• 그래프의 한 종류. ‘최소 연결 트리’라고도 불림.
• 사이클 불가능
• 노드가 N개인 트리는 항상 N-1개의 간선을 가진다.
• 한 개의 루트 노드만이 존재하며 모든 자식 노드는 한 개의 부모 노드만을 가진다.

트리 구성 요소

• Node (노드): 트리를 구성하고 있는 각각의 요소를 의미
• Edge (간선): 노드와 노드를 연결하는 선
• Root Node (루트 노드): 최상위에 있는 노드
• Terminal Node(= leaf Node, 단말 노드): 하위에 다른 노드가 연결되어 있지 않은 노드
• Internal Node (내부노드, 비단말 노드): 단말 노드를 제외한 모든 노드

Binary Tree (이진 트리)

루트 노드를 중심으로 두 개의 서브 트리로 나뉘어 진다. 또한 나뉘어진 두 서브 트리도 계속 모두 이진 트리. 트리에서는 각 층별로 숫자를 매겨서 이를 트리의 Level(레벨)이라고 한다. 레벨의 값은 0 부터 시작해 루트 노드의 레벨은 0이다. 그리고 트리의 최고 레벨을 가리켜 해당 트리의 height(높이) 라고 한다.

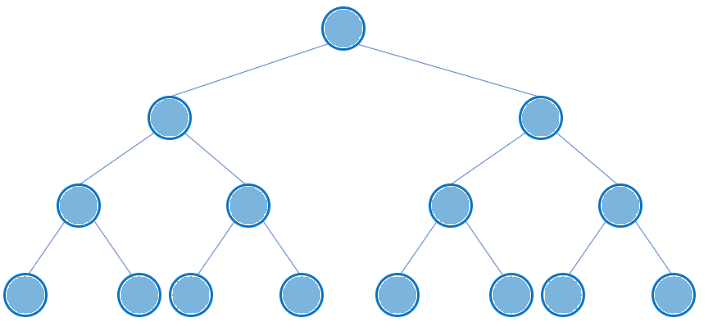
Perfect Binary Tree (포화 이진 트리)

모든 레벨이 꽉 찬 이진 트리

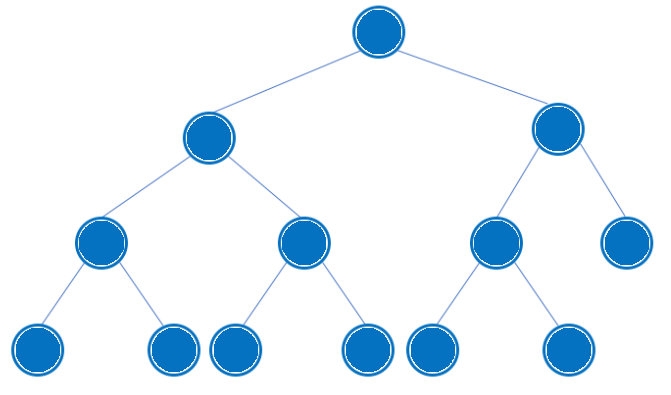
Complete Binary Tree (완전 이진 트리)

위에서 아래로, 왼쪽에서 오른쪽으로 순서대로 채워진 이진 트리

Full Binary Tree (정 이진 트리)

모든 노드가 0개 혹은 2개의 자식노드만을 갖는 이진 트리

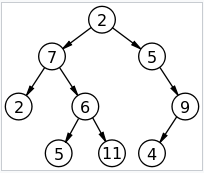
BST (Binary Search Tree)

이진트리의 일종으로 효율적인 탐색을 위한 저장방법. 단 이진 탐색 트리에는 데이터를 저장하는 규칙이 있다.

1. 이진 탐색 트리의 노드에 저장된 키는 유일
2. 부모의 키가 왼쪽 자식 노드의 키보다 크다.
3. 부모의 키가 오른쪽 자식 노드의 키보다 작다.
4. 왼쪽과 오른쪽 서브트리도 이진 탐색 트리

이진 탐색 트리의 탐색 연산은 O(log n)의 시간 복잡도를 갖는다. 최악의 경우 한 쪽으로 만 노드가 추가되는 경우가 발생해 Skewed Tree(편향 트리)가 되면 시간 복잡도가 O(n)이 된다. 이를 해결하기 위해 AVL Tree, Red-Black Tree 같은 Rebalncing 기법이 있다.

*틀린 부분이 있으면 언제든지 말씀해 주시면 공부해서 수정하겠습니다.